查看原题请戳这里
因为在每个城市小A和小B下一个要去的城市是一定的,所以在这道题目中不存在决策的问题。
预处理 最近点和次近点 双向链表 流程:
先把城市按高度排序,然后建立双向链表(每一个城市都指向第一个比它低的城市和第一个比它高的城市)。
按照从左到右的顺序去预处理每一个城市的最近点和次近点。
我们按从左到右的顺序去预处理每一个城市的最近点和次近点,因为每一个城市都只能到它右边的城市,而我们又是按照从左到右的顺序进行枚举,那么在当前城市$x$后面的城市无论如何都无法到达$x$,所以我们每处理完一个城市的最近点和次近点就把该城市在双向链表中删除,以保证当处理到城市$x$时,对于双向链表中的所以点$y_i$,都在城市$x$的右侧。
那么,具体怎么通过双向链表去求每一个点的最近点和次近点呢?
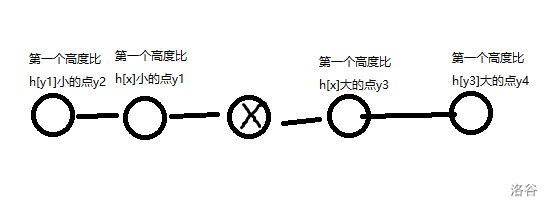
如图,在双向链表中,x的最近点肯定在这4个点中,我们每次只需要在这4个点中选择和x高度差最小的点和次小的点即可。
时间复杂度:$O(n)$
code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void make_dis () a[n + 1 ].u = n + 1 ; for (int i = 1 ; i <= n; i++) a[i].u = i, a[i].h = h[i]; sort(a + 1 , a + n + 1 , cmp1); for (int i = 1 ; i <= n; i++) las[a[i].u] = a[i - 1 ].u, nex[a[i].u] = a[i + 1 ].u; for (int i = 1 ; i <= n; i++) { t[1 ].h = t[2 ].h = t[3 ].h = t[4 ].h = INF; if (las[i] && las[i] <= n) t[1 ].h = h[las[i]] - h[i],t[1 ].u = las[i]; if (las[las[i]] && las[las[i]] <= n) t[2 ].h = h[las[las[i]]] - h[i],t[2 ].u = las[las[i]]; if (nex[i] <= n && nex[i]) t[3 ].h = h[nex[i]] - h[i],t[3 ].u = nex[i]; if (nex[nex[i]] <= n && nex[nex[i]]) t[4 ].h = h[nex[nex[i]]] - h[i],t[4 ].u = nex[nex[i]]; for (int i = 1 ; i <= 4 ; i++) if (t[i].h < 0 ) t[i].h = - t[i].h; sort(t + 1 , t + 5 , cmp1); to[i][0 ] = t[1 ].u; to[i][1 ] = t[2 ].u; d[i][0 ] = t[1 ].h; d[i][1 ] = t[2 ].h; if (las[i] > 0 ) nex[las[i]] = nex[i]; if (nex[i] <= n) las[nex[i]] = las[i]; } }
set set也可以完成这步预处理,原理和双向链表的原理一样,这里就不赘述了。
时间复杂度:$O(n\log n)$
倍增预处理
$f[i][j]$表示从城市$i$出发小A和小B各开车$2^j$次能到达的城市
$g[i][j]$表示从城市$i$出发小A开车$2^j$次行驶的距离
$l[i][j]$表示从城市$i$出发小B开车$2^j$次行驶的距离
初始化:
1 2 for (int i = 1 ; i <= n; i++) f[i][0 ] = to[to[i][1 ]][0 ];for (int i = 1 ; i <= n; i++) g[i][0 ] = d[i][1 ], l[i][0 ] = d[to[i][1 ]][0 ];
预处理:
1 2 3 4 5 6 7 for (int j = 1 ; j <= 21 ; j++) for (int i = 1 ; i <= n; i++) { f[i][j] = f[f[i][j - 1 ]][j - 1 ]; g[i][j] = g[i][j - 1 ] + g[f[i][j - 1 ]][j - 1 ]; l[i][j] = l[i][j - 1 ] + l[f[i][j - 1 ]][j - 1 ]; }
求行驶距离 这里求距离的方法和普通的倍增没有什么区别,但是由于我们记录的是小A和小B每人开$2^j$次的相关数据,所以最后还要判断一下小A自己是否还能再开一次。
code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int get (int s) int j = 0 , hav = x; cnt1 = 0 , cnt2 = 0 ; while ((1 << j) < n) j++; for (; j >= 0 ; j--) if (g[s][j] + l[s][j] <= hav && f[s][j] != 0 ) { hav = hav - g[s][j] - l[s][j]; cnt1 += g[s][j]; cnt2 += l[s][j];s = f[s][j]; } if (d[s][1 ] <= hav && to[s][1 ] != 0 ) cnt1 += d[s][1 ], s = to[s][1 ]; if (cnt2 == 0 ) now = INF; else now = cnt1 / cnt2; return s; }
询问 Q1 求比值最小,我们直接枚举每一个城市作为起点使两者开车的比值即可。
Q2 直接求行驶距离即可。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 #include <iostream> #include <cstring> #include <cstdio> #include <cmath> #include <algorithm> #define ll long long #define INF 1000000000000 #define re register #define int long long using namespace std ;int read () register int x = 0 ,f = 1 ;register char ch; ch = getchar(); while (ch > '9' || ch < '0' ){if (ch == '-' ) f = -f;ch = getchar();} while (ch <= '9' && ch >= '0' ){x = x * 10 + ch - 48 ;ch = getchar();} return x * f; } int n,x,h[1000005 ],s,f[1000005 ][35 ],g[1000005 ][35 ],l[1000005 ][35 ],to[1000005 ][2 ],las[1000005 ],nex[1000005 ];int d[1000005 ][2 ],hb; double ans,now,cnt1,cnt2;struct node { int u,h; }a[100005 ],t[5 ]; bool cmp1 (node x, node y) return x.h < y.h;}bool cmp2 (int x,int y) return x < y;}void init () n = read(); for (int i = 1 ; i <= n; i++) h[i] = read(); } int dist (int x,int y) return abs (h[x] - h[y]);}void make_dis () a[n + 1 ].u = n + 1 ; for (int i = 1 ; i <= n; i++) a[i].u = i, a[i].h = h[i]; sort(a + 1 , a + n + 1 , cmp1); for (int i = 1 ; i <= n; i++) las[a[i].u] = a[i - 1 ].u, nex[a[i].u] = a[i + 1 ].u; for (int i = 1 ; i <= n; i++) { t[1 ].h = t[2 ].h = t[3 ].h = t[4 ].h = INF; if (las[i] && las[i] <= n) t[1 ].h = h[las[i]] - h[i],t[1 ].u = las[i]; if (las[las[i]] && las[las[i]] <= n) t[2 ].h = h[las[las[i]]] - h[i],t[2 ].u = las[las[i]]; if (nex[i] <= n && nex[i]) t[3 ].h = h[nex[i]] - h[i],t[3 ].u = nex[i]; if (nex[nex[i]] <= n && nex[nex[i]]) t[4 ].h = h[nex[nex[i]]] - h[i],t[4 ].u = nex[nex[i]]; for (int i = 1 ; i <= 4 ; i++) if (t[i].h < 0 ) t[i].h = - t[i].h; sort(t + 1 , t + 5 , cmp1); to[i][0 ] = t[1 ].u; to[i][1 ] = t[2 ].u; d[i][0 ] = t[1 ].h; d[i][1 ] = t[2 ].h; if (las[i] > 0 ) nex[las[i]] = nex[i]; if (nex[i] <= n) las[nex[i]] = las[i]; } } void make_bz () for (int i = 1 ; i <= n; i++) f[i][0 ] = to[to[i][1 ]][0 ]; for (int i = 1 ; i <= n; i++) g[i][0 ] = d[i][1 ], l[i][0 ] = d[to[i][1 ]][0 ]; for (int j = 1 ; j <= 21 ; j++) for (int i = 1 ; i <= n; i++) { f[i][j] = f[f[i][j - 1 ]][j - 1 ]; g[i][j] = g[i][j - 1 ] + g[f[i][j - 1 ]][j - 1 ]; l[i][j] = l[i][j - 1 ] + l[f[i][j - 1 ]][j - 1 ]; } } int get (int s) int j = 0 , hav = x; cnt1 = 0 , cnt2 = 0 ; while ((1 << j) < n) j++; for (; j >= 0 ; j--) if (g[s][j] + l[s][j] <= hav && f[s][j] != 0 ) { hav = hav - g[s][j] - l[s][j]; cnt1 += g[s][j]; cnt2 += l[s][j];s = f[s][j]; } if (d[s][1 ] <= hav && to[s][1 ] != 0 ) cnt1 += d[s][1 ], s = to[s][1 ]; if (cnt2 == 0 ) now = INF; else now = cnt1 / cnt2; return s; } void fri_query () int u = 0 ; x = read(); ans = 9999999999.9 ; for (int i = 1 ; i <= n; i++) { now = 0.0 ; get(i); if (ans > now) ans = now,u = i; if (ans == now && h[u] < h[i]) ans = now,u = i; } printf ("%d\n" ,u); } void sec_query () int m = read(); for (int i = 1 ; i <= m; i++) { s = read(); x = read(); get(s); printf ("%.0lf %.0lf\n" ,cnt1,cnt2); } } signed main () init(); make_dis(); make_bz(); fri_query(); sec_query(); return 0 ; }