path
考虑直接在 DFS 整棵树的过程中构造哈密尔顿回路。
先考虑如果是一条链怎么构造,我们可以隔一个跳一下,就像这样:
那么这样构造我们只需要用到距离不超过 2 的边,所以直接拓展到树上即可:如果当前节点深度是奇数,那么我们在 DFS 前输出这个点,否则在 DFS 完所有孩子之后再输出这个点。容易验证这样构造是对的。
时间复杂度: $Θ(n)$。
magic
首先,使用 KMP 算法对于每个 Ti,求出它在 S 中的匹配位置,那么这些位置中至少得要挖掉一个。
于是对于每个 i,我们可以求出一个 Li,表示 [Li, i] 之间必须要挖掉至少一个。
然后我们考虑 DP,设 fi 表示最后一个挖掉的位置是 i 的最小代价,那么转移时枚举上一个挖掉的位置即可做到时间复杂度 $Θ(n^2)$。
考虑优化。注意到我们在转移时一定是整体转移,而每次可能非法化一个前缀。因此,如果我们不再进行非法化,那么可以转移的区间就是原序列的一个后缀,因此我们可以变为后缀查询最小值、单点修改。直接使用树状数组维护即可。
时间复杂度: $Θ (nlog_2n+∑_{i=1}^m(|S| + |Ti|))$。
inter
可以发现 u, v 是独立的。我们等价于要求:在 u 的子树中选 k 个点使它们两两LCA 是 u 的方案数,对 v 也求同样的东西,再把两者相乘就是最后的答案了。
如果 u, v 存在祖孙关系,不妨设 u 是 v 的祖先,那么 u 的子树就要改为以 v 的方向作为根方向前提下的子树。
显然为了使两两 LCA 是 u,在 u 的每一个儿子中就至多只能选一个点。于是我们做一个背包,就可以得到以 u 作为根的时候选择 k ≤ L 个点的方案数,然后选择 u的方案直接枚举 u 被选了多少次,做一个组合数即可。
但是我们这样求出的是以 u 为根的方案数,其中可能会有的点选在了 u → v 的方向上,这样就不满足条件了。
考虑这个背包的实质,可以发现他求的是下列生成函数的 xk 项的系数:
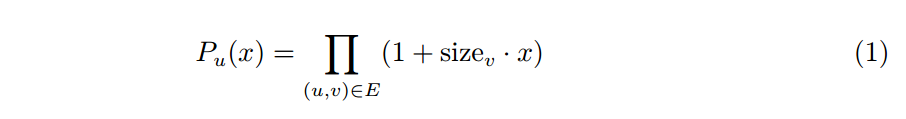
那么我们现在要求的是不在 v 方向的多项式 Pu,v(x),他的式子如下:
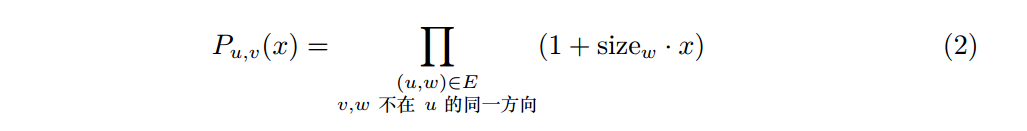
则可以发现 Pu,v(x) 就是 Pu(x) 除掉一个 (1 + sizew · x) 之后的结果,其中 w 是u 在 v 方向的出边。可以发现,多项式除以单项式其实就是背包的过程倒过来,直接做就可以做到线性复杂度。
时间复杂度: $Θ((n + q)L + qk)$。

