前言

SPFA算法由于它上限O(NM)的时间复杂度,被卡掉的几率很大.在算法竞赛中,我们需要一个更稳定的算法:dijkstra

什么是dijkstra?

dijkstra是一种单源最短路径算法,时间复杂度上限为O(n^2)(朴素),在实际应用中较为稳定;加上堆优化之后更是具有O((n+m)log^2 n)的时间复杂度,在稠密图中有不俗的表现.

dijkstra的原理/流程?

dijkstra本质上的思想是贪心,它只适用于不含负权边的图.
我们把点分成两类,一类是已经确定最短路径的点,称为”白点”,另一类是未确定最短路径的点,称为”蓝点”

dijkstra的流程如下:

初始化dis[start] = 0,其余节点的dis值为无穷大.
找一个dis值最小的蓝点x,把节点x变成白点.
遍历xx的所有出边(x,y,z)，若dis[y] > dis[x] + z,则令dis[y] = dis[x] + z
重复2,3两步,直到所有点都成为白点.
dijkstra为什么是正确的
当所有边长都是非负数的时候,全局最小值不可能再被其他节点更新.所以在第2步中找出的蓝点x必然满足:dis[x]已经是起点到x的最短路径.我们不断选择全局最小值进行标记和拓展,最终可以得到起点到每个节点的最短路径的长度
图解
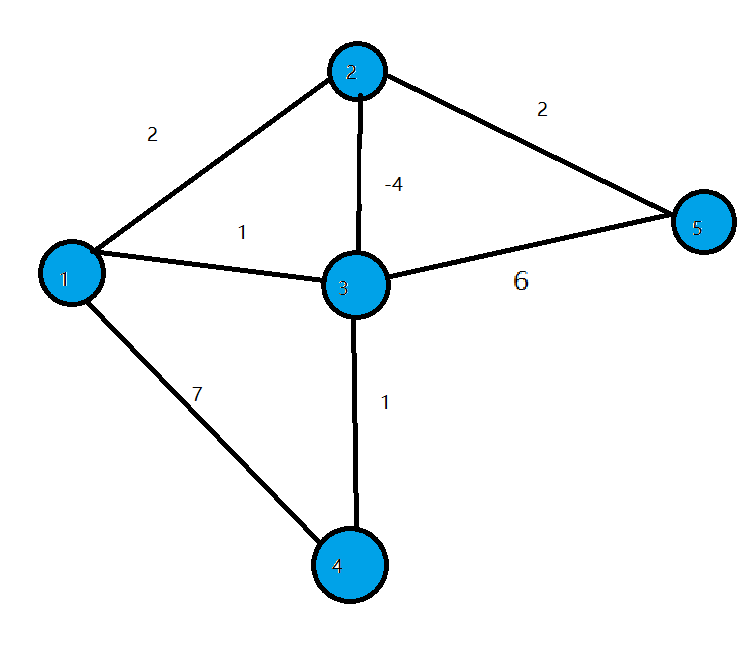
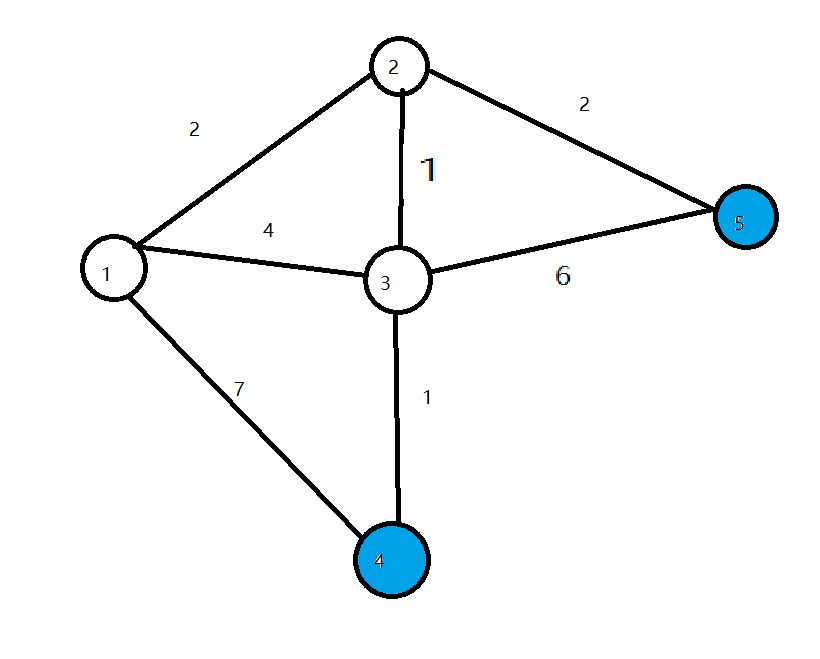
(令start = 1)
开始时我们把dis[start]初始化为0,其余点初始化为inf

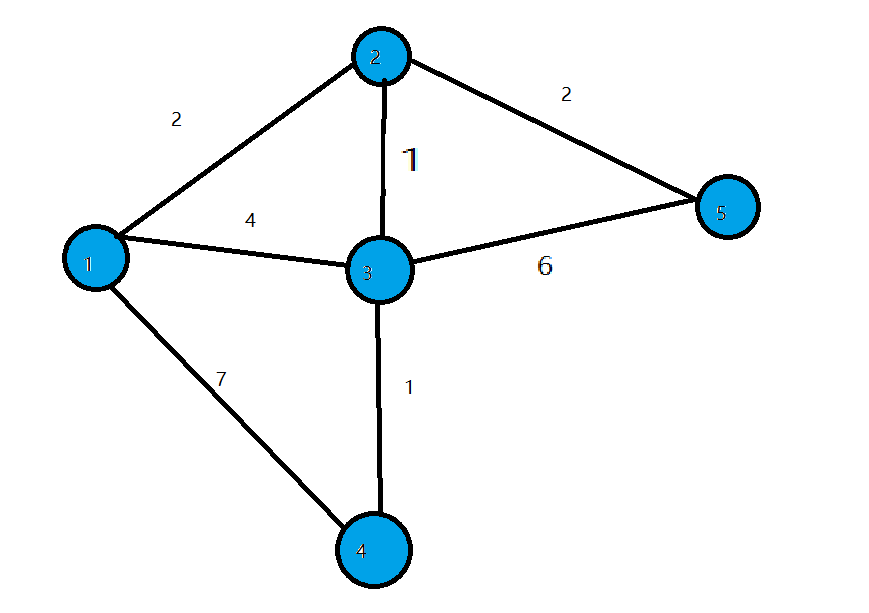
第一轮循环找到dis值最小的点1,将1变成白点,对所有与1相连的蓝点的dis值进行修改,使得dis[2]=2,dis[3]=4,dis[4]=7

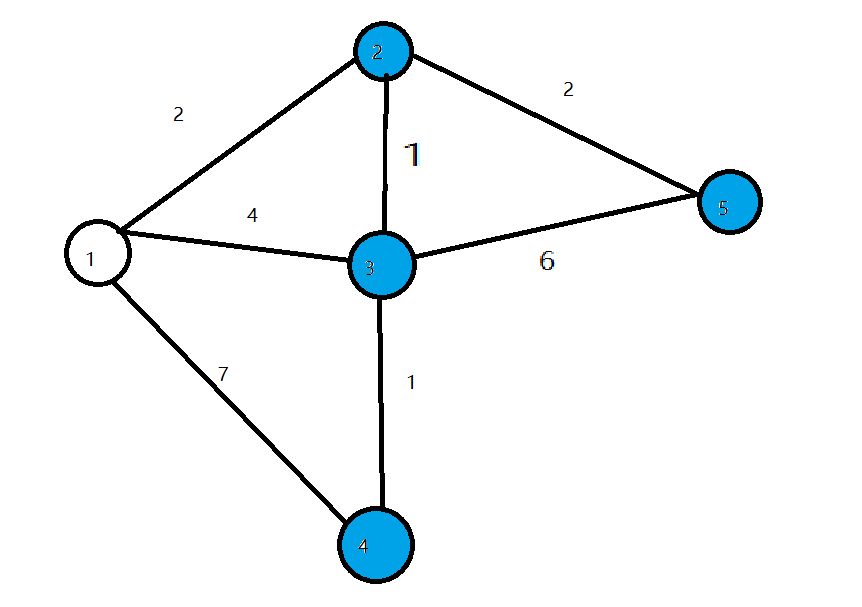
第二轮循环找到dis值最小的点2,将2变成白点,对所有与2相连的蓝点的dis值进行修改,使得dis[3]=3,dis[5]=4

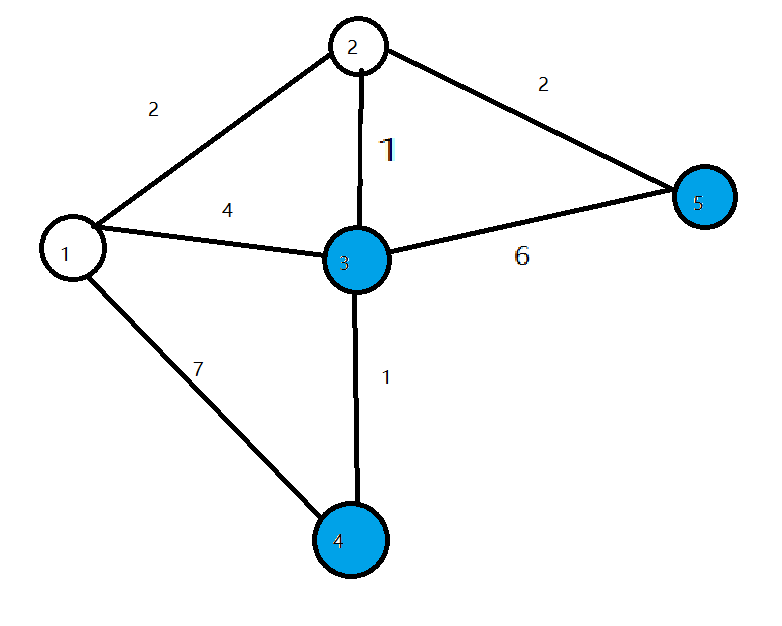
第三轮循环找到dis值最小的点3,将3变成白点,对所有与2相连的蓝点的dis值进行修改,使得dis[4]=4

接下来两轮循环分别将4,5设为白点,算法结束,求出所有点的最短路径

为什么dijkstra不能处理有负权边的情况?

我们来看下面这张图

2到3的边权为−4,显然从1到3的最短路径为−2 (1->2->3).但在循环开始时程序会找到当前dis值最小的点3,并标记它为白点.
这时的dis[3]=1,然而1并不是起点到3的最短路径.因为3已经被标为白点,所以dis[3]不会再被修改了.我们在边权存在负数的情况下得到了错误的答案.

dijkstra的堆优化?

观察dijkstra的流程,发现步骤2可以优化
怎么优化呢?
我们可以用堆对disdis数组进行维护,用O(logn)的时间取出堆顶元素并删除,用O(logn)的时间遍历每条边,总复杂度O((n+m)\log^2 n).
附一下代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#define ll long long
#define INF 2147483647

using namespace std;

struct node{
    int k,dis;
    bool operator < ( const node &x )const{return x.dis < dis;}
};

priority_queue<node> que;

long long n,m,s,d[1000005],cnt,D[1000005],v[1000005]; 

struct Edge{
    int to,next,x;
}edge[2000005];

void add(int x,int y,int a)
{
    edge[++cnt].to = y;
    edge[cnt].x = a;
    edge[cnt].next = d[x];     
    d[x] = cnt;
}

int main()
{
    int x,y,a;
    scanf("%lld%lld%lld",&n,&m,&s);
    for(register int i = 1; i <= m; i++)
    {
        scanf("%d%d%d",&x,&y,&a);
        add(x,y,a);
    }
    que.push((node){s,0});
    for(register int i = 1; i <= n; i++) D[i] = INF;
    D[s] = 0;
    while(!que.empty())
    {
        node u = que.top();
        que.pop();
        if(v[u.k]) continue;
        v[u.k] = 1;
        for(register int i = d[u.k]; i; i = edge[i].next)
        {
            if(D[edge[i].to] > D[u.k] + edge[i].x)
            {
                D[edge[i].to] = edge[i].x + D[u.k];
                if(!v[edge[i].to]) que.push((node){edge[i].to,D[edge[i].to]});
            }
        }
    }
    for(register int i = 1; i <= n; i++) printf("%d ",D[i]);
    printf("\n");
    return 0;
}